確率密度関数f(x)は区間[a,b]の場合は f(x)=1/(b-a)、
それ以外の区間では0
と書かれている。上記の例ではa=0、b=360となるので
f(x)=1/360 という定数になる。この1/360は確率密度であって確率ではない。確率は確率密度を一定の区間で積分して求めなければならない。 上記の例ではx=60の確率を知りたいので定積分してみると
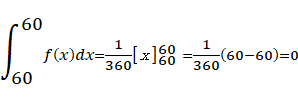
となり確率はゼロとなる。連続確率変数の場合は特定の値についての確率はゼロとなり、確率は区間を定めて確率密度関数を積分して計算しなければならない。一様分布に限らず正規分布などの他の連続確率変数の場合も同様に特定の値についての確率はゼロとなる。これについては感覚的な説明の仕方として、サイコロの例だと1から6までの6個の数字のどれが出るかという計算なので確率計算する場合の分母の数は6という有限値なので1÷6という計算が出来るが、連続変数の時計の例では区間が0から360までとなっているが、この区間に存在にする数字は0.01、0.001,359.9999など無数の実数が稠密(ちゅうみつ)に詰まっているので実数の個数としては無限大となるので、その中からピンポイントで1つに値を当てる確率は 1/∞=0 と考えることが出来る。いいかげんなことを書き綴っているように見えるかも知れないが、このような説明は統計学の専門家でもされている。例えば、古い本になるが、統計学通論 北川敏男ほか 共立出版株式会社 1990年10月などがある。最近の書籍ではWilliam E, Griffithsほかの Principles of econometrics Wiley 2018 でも似たような説明がされている。Griffithsはベイズ統計学者としても著名でこのPrinciples of econometricsは基本的なところを、かゆいところに手が届くような説明がなされており大変に気に入っており、基本書としてお世話になっている。ペーパーバック版だと少し安く買えるが、本箱に立てようとすると、すぐに倒れてしまうのが唯一の難点といえるだろう。真面目にこの問題を考えてゆくと実数体系の連続性の問題に関係してくると思う。文系向けに書かれた数学書シリーズで経済数学教室 小山昭雄 岩波書店 1994 があるが、このシリーズの3 線型代数と位相 上で デデキンド(Dedekind)の「切断」のことが書かれている。残念ながら何回読んでみてもよく理解できない。小生のような凡人ができるだけ数学的に厳密に理解したいとあちこち首を突っこむと結局、時間だけが過ぎてしまい本来の目的とする専門分野の勉強がおろそかになるというディレンマに陥ってしまう。今にして反省すれば、もっと時間配分、労力配分を工夫しておけばよかったとつくづく思う次第である。
二変数の一様分布(周辺分布、たたみ込み)の復習をしてみる
次に2変数の一様分布について考えてみる。xとyの2個のサイコロを同時に振って出る目の分布を考える。サイコロxの目は1から6までで、公正なサイコロであれば、目の出方は1/6の一様分布をしている。サイコロyも同様である。xとyの組合せは6×6=36通りある。つまり2個のサイコロを同時に振ったときの同時確率は1/36の一様分布をしている。表にまとめれば次のようになる。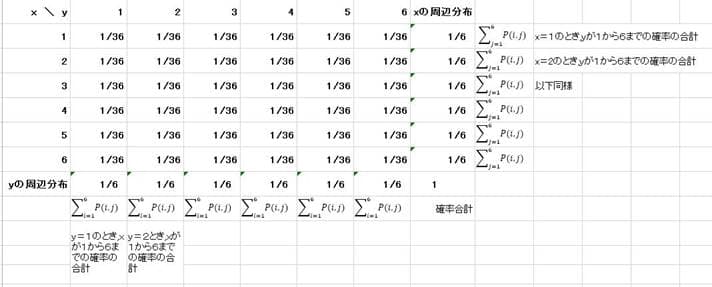
xとyの周辺分布は1/6の一様分布で、xとyの同時分布は1/36の一様分布になっている。xとyは独立しているのでxの周辺分布×yの周辺分布=x、yの同時分布の関係が成り立っている。この話を少しアレンジして2個のサイコロを同時に振ったときの出る目の和の分布を考えてみる。つまりx+yの確率分布はどのようなものになるかを見てみる。これを表にまとめると次のようになる。
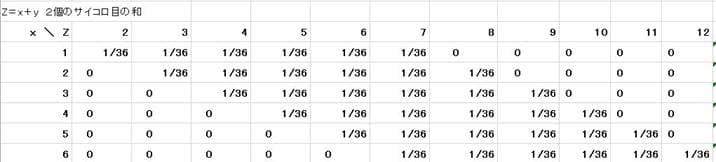
2個のサイコロの和は最小値が1+1=2で最大値は6+6=12の間になる。各目の合計zは7となる確率が最大となっている。度数分布表にまとめて整理すると 次のようになる。
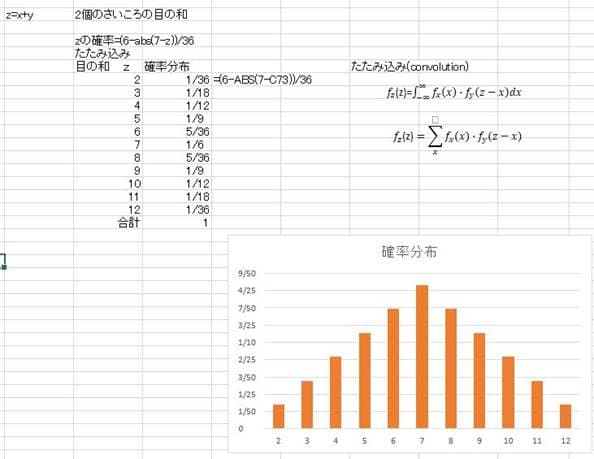
サイコロx、yの目は一様分布に従う確率変数で目の和は確率変数xとyの合計(zで示す)も確率変数である。確率変数の話になると面倒なことに2+3=5といった計算が出来ない。xもyも一様分布といった確率分布に従って実現値が出てくるので単純な足し算が出来ない。幸にもxとyが独立であればたたみ込み(convolution)といった数学的な操作をしてx+y=zの確率分布を求めることが出来る。(なお、数学的な話は数学のテキストや数学専門のサイトで正確な説明を参照されたい)上記の表はたたみ込みをしてzの確率分布を求めたものである。直感的に考えるとサイコロも目の出方は均一なので、その合計値も2から12までも等確率になりそうなものだが、意外にもz=7を頂点とする三角分布になっている。サイコロの話というと子供の宿題を手伝っているようで面白くないという人もいるかもしれないが、サイコロをx株とy株と読み替えれば少し現実味が出てくる。x株とy株は何らの依存関係もなく独立に変動し、それぞれの株価は1千円から6千円の間でまんべんなく変動するレンジ相場の状態にあるとすれば、月末時点での手持ちポートフォリオ(x+y)はどのような確率分布になるだろうかという問題になる。確率分布から見ると7千円の確率が高いのではと言うことになる。
確率積分変換について視覚的に考えてみる
一様分布については、見方を変えると各種の確率分布(累積分布)は一様分布に射影されることがわかる。統計ソフトRには様々な確率分布関数が装備されているので標準正規分布を例にとって見てみる。よくテキストの出てくるグラフは釣鐘状の確率密度関数のグラフだが、ここでは下記のような累積密度関数(確率分布)のグラフを見てみる。 なお、z値は(x-平均値)/標準偏差でz変換された(標準化または規準化されたとも言う)数値を示す。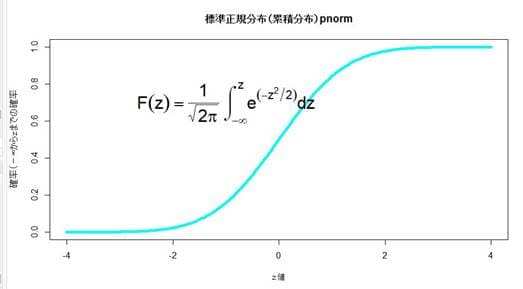
この逆関数は以下のようなグラフとなる。数学的にややこしい話は抜きにして言えば、逆関数とは、例えば f(x)=7*X の逆関数はf⁻¹(x)=1/7*X となり、きれいな数式で表せる。しかし正規分布関数は複雑で、その逆関数はきれいな数式では表せないので数値計算で近似計算することになる。幸にも、統計ソフトではそのような計算をしてくれる関数が準備されており、Rではqnormはpnormなどの関数が使える。
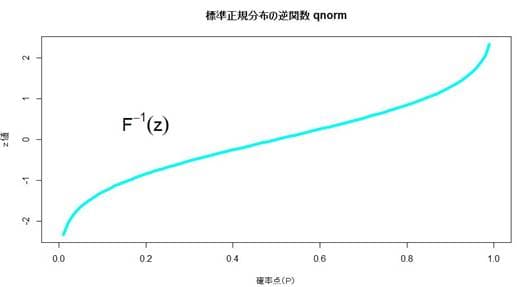
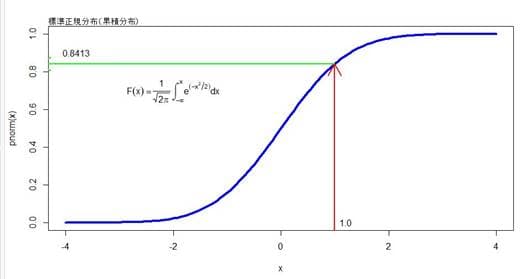
正確に描けばxの変域は-∞から∞と左右に広がっているので教科書の紙面を無限に大きくはみ出してしまう。人間には無限は自由に扱えないので数学的には何らかの工夫をして近似計算することになる。x=-4辺りでもpnorm(-4)≒ 3.167124e-05と実用上は十分にゼロに近い。標準正規分布(累積分布)のグラフのy軸の方を見ると累積分布はゼロから1までの間で一様分布していることが分かる。平均値0近辺は密度が高いところだが、その当たりのカーブは急な曲がり方をしており、また密度が低い下部と上部の曲がり方はカーブが平坦となっており、万遍なく[1-0]の区間に分布していることがわかる。一様分布で区間(0-1)の任意の数値、例えば8.413を選んだとすればy軸から緑色の線がF(x)と交叉する点を求め、そこから赤色の線がx軸に交叉する点が標準正規分布の対応するz値(ここの例では1)となる。つまり一様分布の数値から正規分布の数値に変換したことになる。この原理を使えば一様分布乱数から様々な分布の確率変数の乱数を生成することができる。これは確率積分変換と呼ばれている。同じことだが逆関数からも同様の計算ができる。
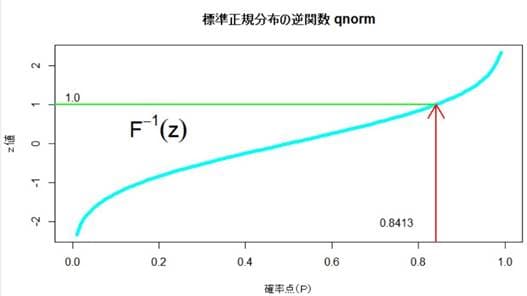
逆関数の場合はx軸からみると区間(0-1)で一様分布していることがわかる。Rではqnormはpnormの逆関数となっておりpnorm(1)=0.8413, qnorm(0.8413)=0.9998≒1となり、またpnorm(qnorm(0.8413)=0.8413と計算できるのでこの関係を確認できる。これはシミュレーションの基本的な考え方となっており、一様分布と特定の分布関数を与えればどの様な分布も生成できるという意味で一様分布は基本的な役割を果たしている。
ほんの少しだけ、コピュラ(接合分布関数)をグラフで眺めてみる
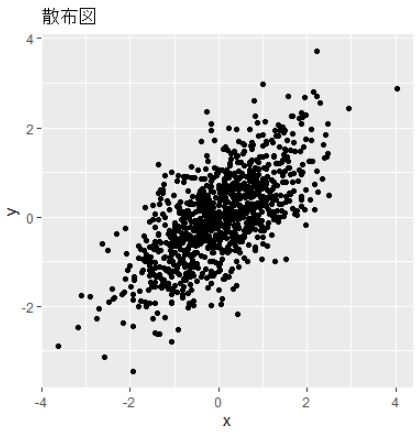
ここで再びサイコロの話しに戻るが、xとyは相互の独立という前提での話だった、xとyに何等かの依存関係があり、例えばxが小さい数の目が出るときにはもう一方yも小さい数の目が出る傾向があるような場合にはどのように表現できるのだろうか。確率論のテキストでは同時分布から周辺分布を導出する方法は書かれているが、独立でない周辺分布から同時分布を求める方法はあまり言及されていないようだ。しかし、うまい具合に、1つ考え方としてコピュラ(接合分布関数)を使う方法があるようだ。コピュラについては数学的な定義は難しいが、 n個の変数でなく2変数の例に狭めて考えると、大ざっぱに言えば、xとyの2変数からなる同時分布関数(累積分布)H(x、y)があり、その周辺分布関数(累積分布)を一様分布であるF(x)とG(y)とすると、 H(x、y)=C(F(x),G(y))が成り立つようにする接合分布関数(コピュラ)が存在することが知られている。イメージで表すと同時分布=コピュラ+周辺分布 の関係が成り立つようにする接合関数が存在することを示している。どんな関数でも接合関数として使えるというわけではなく、連続性とか共単調(comonotone)とか単調変換の下での不変性とか様々な数学的な特性を備えていることが必要となる。このような数学的特性を備えた接合関数としては正規コピュラ、tコピュラ、アルキメデス型コピュラなどが知られている。数学的にはスクラー(Sklar)の定理などが根拠となっているようだが、詳細は専門書を参照されたい。周辺分布F(x),G(y)も上記のグラフで示した確率積分変換を使えば一様分布F(x)=U,G(y)=V が求められる。従って、その逆関数 x=F⁻¹(U), y=G⁻¹(V)も得られる。ここでH(x、y)のx,yにx=F⁻¹(U), y=G⁻¹(V)をそれぞれ代入すれば同時分布関数H(x,y)のコピュラC(u,v)が得られる。つまり、C(u,v)=H(F⁻¹(U),G⁻¹(V))。数式だけでは分かりにくいので、簡単な計算例でRを使って体験的な学習すると次のようになる。例えば正規分布に従う2変数x、yがあり両者の相関係数が0.7とする標準正規乱数を1000個生成する。それを2次元グラフにすればxとyの同時正規確率分布H(x,y)の散布図が下記のように描ける。
参考までに、相関係数が0.7の2変数の標準正規同時密度と累積分布のグラフを見ておく。後ほどに触れるが正規コピュラの同時密度や同時分布のグラフとは異なったものになっている。2次元標準正規同時密度を天空から見下ろすと等高線が描ける。完全無相関つまり相関係数が0の時には楕円の特殊形である円(真円)の等高線が描け、相関係数が0.7であれば楕円の等高線となる。詳細は統計学のテキストを参照されたい。
標準正規変数の変域は理論的には(-∞,+∞)であるが[-4,4]で近似計算している。先ほど確率積分変換に使った1次元正規分布の2次元バージョンのグラフとなっている。2次元標準正規密度関数を(-∞,+∞)の変域で2重積分していくと最終的に1に収束していくイメージを2次元標準正規同時分布のグラフは表している。
次にxとyについて上記で述べた確率積分変換をしてC(u,v)求めてグラフにすると以下のようになる。
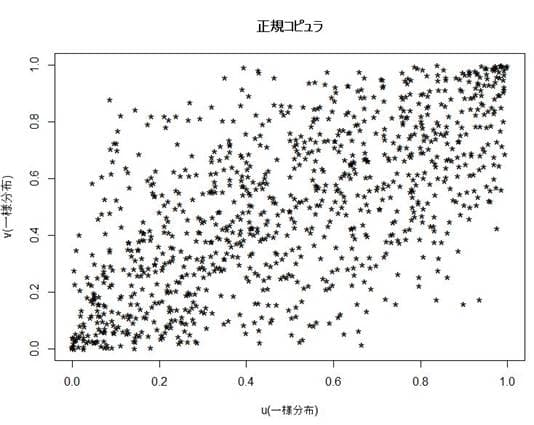
周辺分布も合わせてグラフにしてみるとu,vは各周辺分布が一様分布となっていることが分かる。
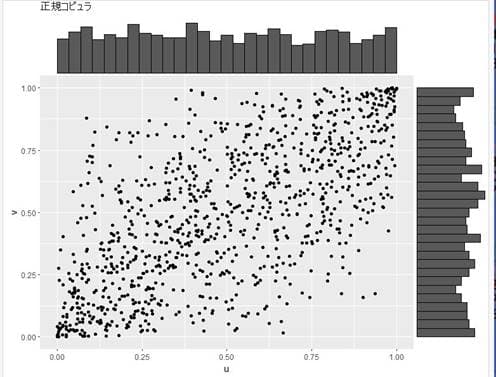
同時分布のグラフを見ると中央部でドットが蜜となっているが、コピュラでは左下(座標軸の0辺り)と右上(座標軸の[1,1])辺りでドットが蜜となっており比較的そこら辺りで依存関係が比較的に高いように見える。このC(u,v)の同時分布は[0-1]の立方体の中にあるが一様分布ではない。
Rのライブラリーのcopulaを使うと、上記と同じ操作が簡単にでき、しかも確率密度関数や累積分布のグラフも下記のように表示できる。
まず標準正規分布に従う相関係数0.7の2変数の乱数を一様分布に変換して、それを正規コピュラ乱数として生成させた数値をグラフにしてみる。
下記のように、この生成された乱数は前者の方法で生成したものと同一となっている。
> head(df1)
u v
1 0.67831670 0.66337274
2 0.07438501 0.07192181
3 0.01026384 0.34820866
> head(uu)
[,1] [,2]
[1,] 0.67831670 0.66337274
[2,] 0.07438501 0.07192181
[3,] 0.01026384 0.34820866
この正規コピュラについての密度関数(PDF)をグラフにすると下記のようになる。
同様にして累積分布(CDF)は下記のようになる。
上記の作業は正規分布乱数を発生させたり、また正規分布関数に投げ込んだりして無駄な作業に見えるかもしれないが、最初に正規分布乱数を発生さたときには、その乱数は正規分布すると共に、その周辺分布も正規分布をしている。コピュラで接合するには周辺分布は一様分布にする必要がある。標準正規変数の変域は-∞から∞であるが、それを変域0から1までの一様分布変数にマッピングして一様分布の周辺分布を生成し、その一様分布を接合関数としての適格性を備えている多変数正規分布関数で接合して、正規コピュラという同時分布を生成している。グラフから見ても一目瞭然で正規コピュラと言っても正規分布の密度関数や累積分布関数の形とは全く異なっており、変数の変域も「0,1」の範囲になっている。表現が数学的に適当かどうかわからないが、素人としてそのようなイメージをもっている。
コピュラについては一般教養書的な書籍が出版されていないようなので、なかなか学習しがたいが、何か大きな可能性を持っているように感じる。一様分布は確率分布の世界では線形代数の単位行列のような意味合いを持っているようで、様々な分布を一様分布に変換したり、あるいは別の分布に再変換したりして、それをまたコピュラを使って新しい同時分布を作り出すといった作業が出来るようだ。以下はあまり参考にならないと思うが一応、拙文を書くのに使ったRコードを示している。